动手深度学习note-7(BERT-来自Transformer的双向编解码器表示)

手撕BERT——从注意力开始

前言：

作为一名初学者，在学习d2l的课程时，整个注意力机制这一部分虽然有代码讲解，但对于自己来说理解难度实在太大，根据课程的内容，多方查阅相关资料，历经九九八十一难，总算是磕磕绊绊的勉强看懂了代码。

本文的代码对d2l中的实现进行了解释，并对部分令初学者难以理解的代码从一个初学者的角度做了修改，修改不求优化代码执行效率(没那个水平)，只求能够以更明了的方式去理解模型的原理

概述：

在BERT之前，在计算机视觉领域已经有在ImageNet上训练的通用模型，通过针对具体的下游任务，修改少量模型参数在较少的数据集上进行训练已经取得了良好的效果。而在NLP领域，还没有这样的通用模型，BERT的目的就是在大量的数据上训练一个通用模型，来通过微调来完成各种下游任务。

为什么能够进行预训练(PreTraining)

按照自己的理解：首先，神经网络的本质上是一个特征提取器，下游的具体任务不同只是如何利用这些特征的问题。我们在整个机器学习或者深度学习中，已经进行了同分布假设，就假定训练样本的数据按照某个相同的分布规律，这样，不同样本在同一位置的数值表示可以共用同一套参数。现在，我们如果在足够大量的数据上有足够多的参数，这样训练的结果就认为学习到了整个大样本的分布规律，提取到了足够多的特征，从而最后获取的特征能够满足不同的任务

类比与让人来识别一个东西是什么，对应的输入经过预训练模型的输出每一个通道就类似于告诉你不同的信息，比如第一个通道是告诉你颜色，第二个通道告诉形状，以此类推，如果这样的信息有足够多，那么，就能有较高的把握判断出要识别的是什么。

基于这样的认识，可以这样认为

  • 在CV任务中，我们认为无论进行什么物体的识别，物体的最主要的特征就只包含输出的通道数这么多个，这些通道数的信息又是之前的各种层在某一方面提取的信息的总和，这样就完成了从图片到特征的压缩，最后如果是分类任务，其实就是基于这些特征的再压缩，得到一个最抽象的结果，而这个结果就是需要的输出
  • 同理，在NLP领域中，对于每一个词，经过预训练模型，同样能够提取到足够的每个词本身以及与其他词的关系的足够多的特征，这些提取到的特征我们认为在最好的情况下是捕捉到了整个句子的所有特征以及内在的语义关系，这些特征就可以拿来完成下游具体的文本任务

模型推导与实现

导入依赖包：

1
2
import torch
from torch import nn

BERT充分借鉴了Transformer的架构，其实其本质就是Transformer的编码器部分，只不过在具体的细节上有略微不同。

BERT的目的是做通用的NLP模型，其目的不再是文本翻译，因此可以认为只有编码器来提取信息而不需要解码器输出。

BERT的数据集是不需要经过标注处理的文本，通过预处理读取一对句子对，通过两个任务（Predict Masked Tokens和Predict Next Sentence）实现自监督学习，由于不需要进行标注，所以可以在非常大量的数据集上进行训练。

Transformer架构

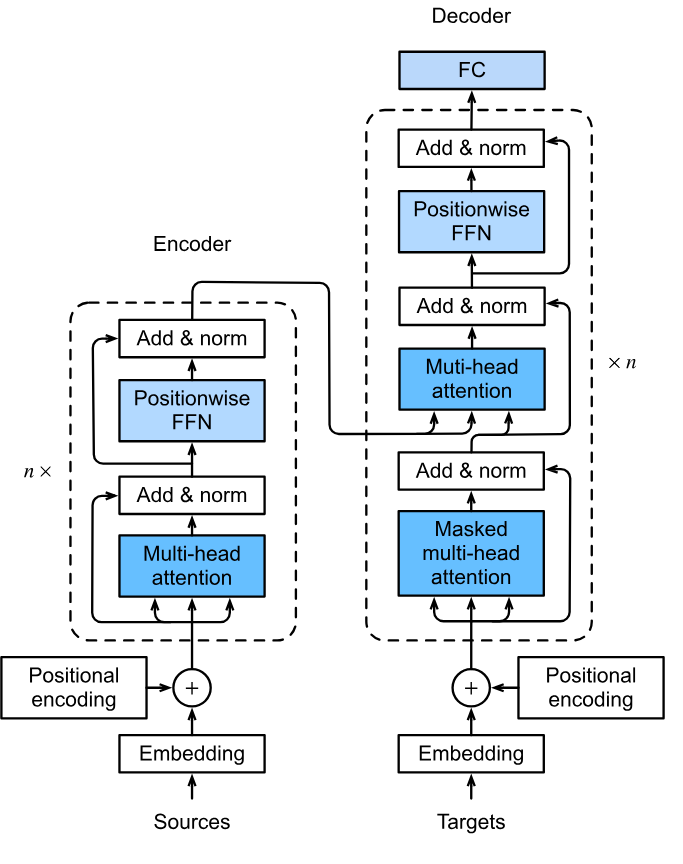
Transformer Architecture

编解码器架构

从整体上看，Transformer使用了编-解码器架构，编码器负责提取信息，解码器负责输出。BERT中没有输出标签，所以自然也没有解码器。

注意力机制(Attention)

这里说一种我最认可的理解：

首先，对于注意力机制的意义应该通过类比人来观察物体来理解

  • 无意识的观察

    无意识的观察

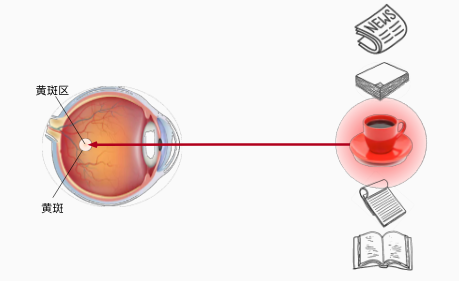
    回忆之前的全连接和卷积，就是类似于人的一种观察，这样观察的结果最好的情况下是有所有的东西的，但是，正如人在无意识的观察的时候不可能能关注到所有的细节，神经网络在做相同的事情时也无法捕捉到所有的信息，捕捉信息的侧重是不同的，这个侧重可能是由物体的特定的形状、颜色是否鲜艳等来特定的特征来决定，通常来说，和人观察一样，卷积和全连接操作通常对颜色较为鲜艳的物体更加敏感。

因此，不难发现，全依靠这种方式不能精准且高效的捕捉到我需要的信息

例如：

图例

在这张图片中，如果我的问题是这是一个什么场景，这样提取到的关于坑的信息就不重要了，虽然后续有全连接层进行选择，但如果这个坑更大可能就会影响模型的判断。

如果让问一个人这是什么场景：

  • 这个人的操作大概是先看清了这是条街，然后才会注意到坑

同样的图片，如果询问这条街道有什么不同：

  • 回答时大概率会立刻注意到有个坑在路中

因此，在有了询问的时候，人看东西就有了目标，会自觉的按着目标去查找有用的信息，这样便有了第二种观察方式。

  • 有意识的观察

    有意识的观察

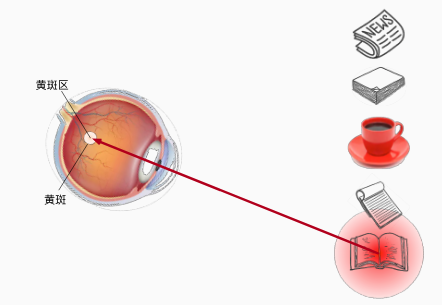
    同样的场景，当明确我要看书的时候，我会去找书而不是杯子，这里捕捉的信息杯子的信息对我来说就不重要了。

    为了模拟这种过程，使用了查询(query)来模拟这种有意识

注意力汇聚

但是，要理解注意力机制具体是怎么算出来的又不能按照注意力来理解，应该按照全局查找\(\rightarrow\)计算权重\(\rightarrow\)加权求和来理解

例：

key value
张三 [1, 2, 0] 18
张三 [1, 2, 0] 20
李四 [0, 0 ,2] 22
张伟 [1, 4, 0] 19

全局查找

如果假设key[0]==1表示姓张，那么要计算平均年龄就可以用

1
2
3
4
dot([1, 0, 0], [1, 2, 0]) = 1
dot([1, 0, 0], [1, 2, 0]) = 1
dot([1, 0, 0], [0, 0, 2]) = 0
dot([1, 0, 0], [1, 4, 0]) = 1

这里的计算结果是1就可以理解为对于查询query（姓张）对这个key的注意力为1，也就是满足匹配信息

计算权重

然后对输出[1, 1, 0, 1]进行\(softmax\)操作，得到的是对每个key的注意力权重

1
softmax([1, 1, 0, 1]) = [1/3, 1/3, 0, 1/3]

计算结果[1/3, 1/3, 0, 1/3]，有三个值为\(\frac{1}{3}\)​，含义为这三个key对query相同权重（因为都姓张），值为0（因为不姓张）则表示这个key对query的注意力为0

加权求和

1
dot([1/3, 1/3, 0, 1/3], [18, 20, 22, 19]) = 19

分别乘上数值value就计算出所有姓张的平均年龄

用数学语言来表示：

query: \(\mathbf{q}\) key: \(\mathbf{k}\) value: \(\mathbf{v}\)

将[1/3, 1/3, 0, 1/3]称作注意力分数，用 \(\alpha(\mathbf{q},\mathbf{k_i})\) 表示，用\(a\)来表示注意力评分函数，可以得到： \[ \alpha(\mathbf{q},\mathbf{k_i})=softmax(a(\mathbf{q},\mathbf{k_i}))=\frac{e^{a(\mathbf{q},\mathbf{k_i})}}{\sum_{j=1}^{m}e^{a(\mathbf{q},\mathbf{k_j})}} \] 得到计算结果的过程称作注意力汇聚，用 \(f(\mathbf{q}, (\mathbf{k_1}\mathbf{v_1}), (\mathbf{k_2}\mathbf{v_2}), ... (\mathbf{k_n}\mathbf{v_n}))\) 来表示注意力汇聚函数 \[ f(\mathbf{q}, (\mathbf{k_1}\mathbf{v_1}), (\mathbf{k_2}\mathbf{v_2}), ... (\mathbf{k_m}\mathbf{v_m}))=\sum_{i=1}^{n}\alpha(\mathbf{q},\mathbf{k_i})\mathbf{v_i}=\sum_{i=1}^{n}\frac{e^{a(\mathbf{q},\mathbf{k_i})}}{\sum_{j=1}^{m}e^{a(\mathbf{q},\mathbf{k_j})}}\mathbf{v_i} \]

自注意力(Self-Attention)

如果现在将所有的query，key，value都用一个输入X来表示，有趣的事情发生了：

注意力评分函数的输出也

注意力评分函数

放缩点积注意力
(Transformer和BERT使用的)

计算公式： \[ a=\frac{\mathbf{Q}\mathbf{K}^{\mathbf{T}}}{\sqrt{d}} \] 注意力分数： \[ \alpha(\mathbf{q},\mathbf{k_i})=softmax(a(\mathbf{q},\mathbf{k_i}))=softmax(\frac{\mathbf{Q}\mathbf{K}^{\mathbf{T}}}{\sqrt{d}}) \] 这种注意力需要\(\mathbf{Q}\)，\(\mathbf{K}\)具有相同的嵌入维度d：

即：

参数 形状
\(\mathbf{Q}\) (batch_size x n x d)
\(\mathbf{K}\) (batch_size x m x d)
\(\mathbf{Q}\mathbf{K}^{\mathbf{T}}\) (batch_size x n x m)
即每一个查询字符对每一个K中的字符的注意力

为什么要除以\(\sqrt{d}\)，这里从实际的效果来演示，从数学的角度推导参见数学推导。

首先，建立一个基本的认识，\(softmax\)将输入置为\((0, 1)\)​之间的一个数，输入数值越大越接近1，例如：

1
2
3
4
# 生成一组演示样本
Q = torch.randn((1,2,4))
K = torch.randn((1,2,4))
score = torch.bmm(Q, K.transpose(1,2))
1
2
3
# 输出：
tensor([[[-1.2134, -0.7983],
      [-6.5540,  0.6934]]])

不使用 \(\sqrt{d}\) 放缩：

1
2
# softmax
torch.nn.functional.softmax(score, dim=-1)
1
2
3
# 输出
tensor([[[3.9769e-01, 6.0231e-01],
      [7.1156e-04, 9.9929e-01]]])

可以看到，数值相对较大的\(softmax\)几乎将其值置为了1，相对小的则几乎为零，而且这里只经过了一次操作，而这样的块有许多个，所以理论上这样的效果还会产生累加，因而，最终的结果可能是某些非常显著的特征被置为1，其他被置为0，这样计算梯度的时候梯度会变得非常小甚至梯度消失，导致这部分参数很难更新。

引入\(\sqrt{d}\)的缩放

1
2
3
# softmax with sqrt(d)
import math
torch.nn.functional.softmax(score/math.sqrt(4), dim=-1) # 4: Q or K shape[-1] -> d
1
2
3
# 输出
tensor([[[0.4483, 0.5517],
      [0.0260, 0.9740]]])

同样的数值，这样计算的结果明显更加合理，没有出现极度靠近1或0的情况

放缩点积注意力代码实现
掩码\(softamx\)模块

实现这部分代码，只需要将公式输入便可，但是，输入的不同样本要求字数相同即num_qkv相同，然而现实中输入的句子不可能每个句子的字数相同，因而在实际中使用的填充Padding。

在进行注意力分数计算的时候，明显的，对于查询query对这部分key的字符的注意力分数应该为0，也就是经过\(softmax\)后对应位置的输出为0，所以，在这部分代码的实现中，必须先来定义一个\(softmax\)函数——带掩码的\(softmax\)来完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def masked_softmax(X, valid_lens):
    """
    掩码注意力，valid_lens:有效长度
    ======Examples=====
    masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))
    tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
         [0.4125, 0.3273, 0.2602, 0.0000]],

        [[0.5254, 0.4746, 0.0000, 0.0000],
         [0.3117, 0.2130, 0.1801, 0.2952]]])
    """
    X_shape = X.shape
    if valid_lens.dim() == 1:
        valid_lens = torch.repeat_interleave(valid_lens, X_shape[1])
    else:
        valid_lens = valid_lens.reshape(-1)
    X = sequence_mask(X.reshape(-1, X_shape[-1]), valid_lens, value=-1e6)
    return nn.functional.softmax(X.reshape(X_shape), dim=-1)

在数据预处理的时候会填充完后会记录下开始填充的位置，然后生成一个和填充相同形状的矩阵，矩阵的值为截断位置的索引。

masked_softmax函数的原理是将掩蔽的位置的值设置为一个非常小的数，这样在\(softmax\)的时候这个数的值就能变为0。

为了找出哪些位置被Padding，这里又构造了一个辅助函数sequence_mask：

1
2
3
4
5
6
def sequence_mask(X, valid_len, value):
    maxlen = X.size(1)
    mask = torch.arange((maxlen), dtype=torch.float32,
                        device=X.device)[None, :] < valid_len[:, None]
    X[~mask] = value
    return X

这是整个Transformer乃至整个BERT实现中非常难以理解的一部分代码，使用到了广播机制。

逐行解读：

首先要理解输入X：

  • 在上一个函数中X表示\(\frac{\mathbf{Q}\mathbf{K}^{\mathbf{T}}}{\sqrt{d}}\)的值，形状为(batch_size, n, m)

    注：在实际中，n和m的值相同，都表示填充后的句子长度

  • 在将参数X传入sequence_mask函数的时候对X进行了reshape：

    X.reshape(-1, X_shape[-1])

    因此，实际上函数输入X的形状为(batch_size x n, m)，也就是将多个维度按顺序堆叠到了一起

第一行maxlen拿到了X的第1为也就是m——key的长度

1
2
mask = torch.arange((maxlen), dtype=torch.float32,
                        device=X.device)[None, :] < valid_len[:, None]

  • 首先，明确两个基本点：

    mask本质上是比较运算，返回的数值应该是True or False

    此处valid_len的形状应该与X.size(0)相同(具体valid_len形状的变化会在介绍后续函数时说明)

  • 以一个直观的例子说明：

    假设maxlen=5：

    1
    2
    3
    4
    sequence = torch.arange((5), dtype=torch.float32)

    # 输出：
    tensor([0., 1., 2., 3., 4.])

    假设valid_len的值为2，即从索引2位置开始就不需要了

    如果batch_size=1，那么valid_len应该为：

    1
    tensor([2., 2., 2., 2., 2.])

    需要被mask的X的形状应该为：(5, 5)

    基于这个示例：

    mask这里的X的思路应该是：每一行，从索引2位置开始就不需要了，将值设为-1e6

    • 正常的实现方式：

      1. 将sequence按行复制valid_len.size(0)=5份 # 按多少句话复制

        1
        sequence = sequence.repeat(5,1)

        1
        2
        3
        4
        5
        6
        # 输出：
        tensor([[0., 1., 2., 3., 4.],
                [0., 1., 2., 3., 4.],
                [0., 1., 2., 3., 4.],
                [0., 1., 2., 3., 4.],
                [0., 1., 2., 3., 4.]])

      2. 将valid_len转置，然后按列复制sequence.size(1)=5份 # 按对多少个字的注意力复制

        1
        valid_len.unsqueeze(0).transpose(0,1).repeat(1,5)

        1
        2
        3
        4
        5
        6
        # 输出：
        tensor([[2., 2., 2., 2., 2.],
                [2., 2., 2., 2., 2.],
                [2., 2., 2., 2., 2.],
                [2., 2., 2., 2., 2.],
                [2., 2., 2., 2., 2.]])

      3. 然后比较sequence和valid_len

        1
        sequence < valid_len

        1
        2
        3
        4
        5
        6
        输出：
        tensor([[ True,  True, False, False, False],
                [ True,  True, False, False, False],
                [ True,  True, False, False, False],
                [ True,  True, False, False, False],
                [ True,  True, False, False, False]])

        可以观察到，每一句话，从索引2开始就被标记为False了，这样，我们成功的根据valid_len筛选出了被Padding的字符

    • 其实，这一个过程能够通过PyTorch的广播机制实现，当比较的两个矩阵的形状不同，广播机制能够自动广播到相同的维度。

      所以，这个过程可以这样实现

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      sequence = torch.arange((5), dtype=torch.float32)
      valid_len = torch.tensor([2,2,2,2,2], dtype=torch.float32)

      # sequence能够按行广播，需要在第0维添加一个维度
      sequence = sequence[None,:]
      # 或： sequence = sequence.unsqueeze(0)

      # valid_len能够按列广播，需要在第1维，添加一个维度
      valid_len = valid_len[:, None]
      # 或： valid_len = valid_len.unsqueeze(1)

      sequence < valid_len

      得到相同的结果：

      1
      2
      3
      4
      5
      tensor([[ True,  True, False, False, False],
              [ True,  True, False, False, False],
              [ True,  True, False, False, False],
              [ True,  True, False, False, False],
              [ True,  True, False, False, False]])

    • 有了筛选的结果，将这boolean的矩阵保存为mask，mash的形状与需要掩蔽的X相同，于是可以这样掩蔽：

      1
      X[~mask] = value

      这里先将mask的元素取反，这样需要mask的位置就为True，因而可以索引出对应X中的值，将这个值设置为value，通常为一个非常小的数

实现放缩点积注意力

有了实现好的掩码注意力模块，正式实现放缩点积注意力就非常容易了

实现了一个DotProductAttention类继承自nn.Module，定义一个初始化函数和前向传播函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class DotProductAttention(nn.Module):
    """
    param:
    q: (n x d)
    k: (m x d)
    v: (m x d)
    out: (n x d)
    =====for example=====
    Input: (batch_size x num_heads, num_qkv, num_hiddens)
    Output: (batch_size x num_heads, num_q, num_hiddens)
    """
    def __init__(self, dropout_rate, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout_rate)

    def forward(self, q, k, v, valid_lens):
        _scores = torch.bmm(q, k.transpose(1, 2)) / math.sqrt(q.shape[-1])
        self.weights = masked_softmax(_scores, valid_lens)
        return torch.bmm(self.dropout(self.weights), v)

另外：还有一种常用的注意力叫做加性注意力(Additive Attention)在d2l课程中提到

在加性注意力中，\(\mathbf{k}\)和\(\mathbf{q}\)不再要求有相同的嵌入维度d，而是由一个单层的全连接层映射到一个相同的维度

计算公式为： \[ a(\mathbf{q},\mathbf{k})=\mathbf{w}_{v}^{\mathbf{T}}tanh(\mathbf{W}_{\mathbf{q}}\mathbf{q}+\mathbf{W}_{\mathbf{k}}\mathbf{k}) \] 理论上效果更好，但据说在实际中差别不大

多头注意力

理解多头注意力

现在，有了基本的注意力模块，终于可以来实现多头注意力了

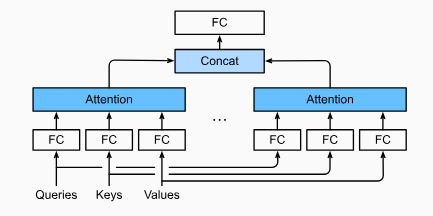
Multi-Head Attention

其实本质上就是一份q,k,v复制成多份，然后每一个”头“的输入q,k,v是原本的q,k,v乘上一个可学习的参数矩阵\(\mathbf{W}_{\mathbf{q,k,v}}\)​，这部分最难理解也是最奇怪的是在具体实现的时候将多个”头“拼接在一起计算，计算的时候做的其实又类似于一个非常大的”单头注意力“。

而所谓的多个头并没有通过复制多份加上多个参数矩阵来完成，而是通过一个参数矩阵映射到num_hiddens维，将num_hiddens维分成num_heads块，每一块我们认为是一个头。然后通过矩阵的形状变换，让不同的头在batch_size这个维度拼接。

同时可以认为构造出的不同的头可以用来分别提取不同类型的输入信息，类似于卷积不同通道的效果。

多头注意力代码实现

为了让”多个头“通过”一个头“来计算，我们必须先来定义两个辅助函数来完成矩阵形状的变换。

1
2
3
4
5
6
7
8
9
10
11
12
13
def transpose_qkv(input, num_heads):
    """
    Input`s shape changes in this method
    1. Input (batch_size, num_qkv, num_hiddens)
    2. temp1 (batch_size, num_qkv, num_heads, num_hiddens/num_heads)
    3. temp2 (batch_size, num_heads, num_qkv, num_hiddens/num_heads)
    4. return (batch_size x num_heads, num_qkv, num_hiddens/num_heads)
    """
    _shape = input.shape
    _temp = torch.reshape(input, (_shape[0], _shape[1], num_heads, -1))  # temp1
    _temp = torch.permute(_temp, (0, 2, 1, 3))  # temp2
    _temp_shape = _temp.shape
    return torch.reshape(_temp, (-1, _temp_shape[-2], _temp_shape[-1]))
1
2
3
4
5
6
7
8
9
10
11
12
13
def transpose_output(output, num_heads):
    '''
    Output shape changes in this method:
    Output: (batch_size x num_heads, num_q, num_hiddens/num_heads)
    temp1: (batch_size, num_heads, num_q, num_hiddens/num_heads)
    temp2: (batch_size, num_q, num_heads, num_hiddens/num_heads)
    return: (batch_size, num_q, num_hiddens)
    '''
    _output_shape = output.shape
    _temp = torch.reshape(output, (-1, num_heads, _output_shape[-2], _output_shape[-1]))  # temp1
    _temp = torch.permute(_temp, (0, 2, 1, 3))  # temp2
    _temp_shape = _temp.shape
    return torch.reshape(_temp, (_temp_shape[0], _temp_shape[1], -1))

然后连接这些函数,实现Multi_Atttention类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Multi_Atttention(nn.Module):
    def __init__(self, num_hiddens,
                 num_heads, dropout_rate, USEBIAS, **kwargs):
        super(Multi_Atttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout_rate)
        self.num_heads = num_heads
        self.attention = DotProductAttention(dropout_rate)
        self.W_q = nn.LazyLinear(num_hiddens)  # (batch_size, num_qkv, num_embeddings) -> (batch_size, num_qkv, num_hiddens)
        self.W_k = nn.LazyLinear(num_hiddens)
        self.W_v = nn.LazyLinear(num_hiddens)
        self.W_o = nn.LazyLinear(num_hiddens,bias=USEBIAS)  # (batch_size, num_q, num_hiddens) -> (batch_size, num_q, num_hiddens)

    def forward(self, q, k, v, valid_lens):
        q = transpose_qkv(self.W_q(q), self.num_heads)
        k = transpose_qkv(self.W_k(k), self.num_heads)
        v = transpose_qkv(self.W_v(v), self.num_heads)
        if valid_lens is not None:
            valid_lens = torch.repeat_interleave(valid_lens, self.num_heads, dim=0)
        output = self.attention(q, k, v, valid_lens)
        return transpose_output(output, self.num_heads)

其中由于多个头其实是按batch_size这个维进行拼接的，因此valid_lens也需要复制num_hiddens份。

Add&Norm层

其实到目前位置，整个解码器的核心已经了解结束了，接下来是一些附加的模块

这一部分就是借鉴了ResNet的思想，使用残差连接来解决梯度消失问题。

假设MultiHeadAttention的作用称作函数\(f\)，输入为\(\mathbf{X}\)，其数学表达为： \[ Normlization(f(x)+x) \] 特别的，在Transformer中使用的\(Normlization\)方法是\(LayerNormlization\)而不是ResNet中使用的\(BatchNormlization\)。

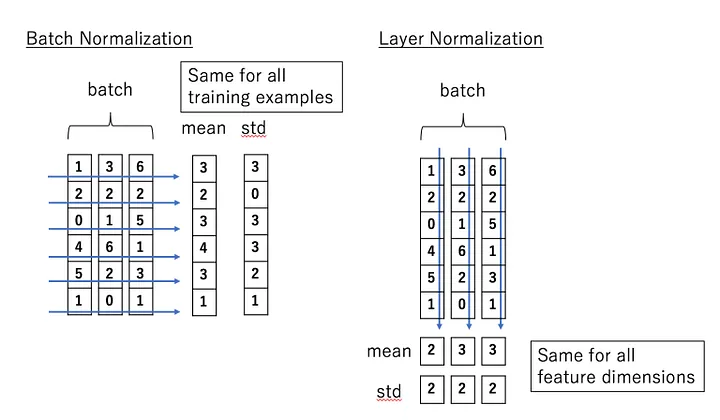
LayerNorm&BatchNorm

一种简单的理解：

图片采用BatchNorm是因为我们认为在图片读取的每一个小批量的信息中不同样本的同一个特征维的数值分布应该大致相同，比如都是纹理信息的表示

而在Transformer中，使用LayerNorm是因为我们认为是同一个样本的所有特征维的数值分布应该是大致相同的，而不同样本的相同特征维关系不大，就比如不同句子在相同的位置的词可能词性都不相同，这样他们的特征维也应该是不同的，因此，还采用BatchNorm是没有意义的，因为应用Norm的数据本身就没有特定的关系

代码实现
1
2
3
4
5
6
7
class Add_Norm(nn.Module):
    def __init__(self, normlized_shape, dropout_rate, **kwargs):
        super(Add_Norm, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout_rate)
        self.layerNorm = nn.LayerNorm(normlized_shape)
    def forward(self, X, Y):
        return self.layerNorm(self.dropout(Y)+X)

基于位置的前馈网络(FFN层)

其实就是两个全连接层，第一个全连接层将样本维从num_hiddens映射到ffn_hiddens，第二个全连接层又将样本维从ffn_hiddens映射回num_hiddens。FFN层使用ReLu作为激活函数。

代码实现
1
2
3
4
5
6
7
8
9
class PositionWiseFFN(nn.Module):
    def __init__(self, ffn_hiddens, ffn_ouputs):
        super().__init__()
        self.dense1 = nn.LazyLinear(ffn_hiddens)
        self.relu = nn.ReLU()
        self.dense2 = nn.LazyLinear(ffn_ouputs)

    def forward(self, X):
        return self.dense2(self.relu(self.dense1(X)))

嵌入层与位置编码

这两部分在BERT中有不一样的实现，这里制作基本的介绍。

在嵌入层中，模型的输入的字符是单个的对应到字典的索引值，嵌入层就是将词索引嵌入到有意义的词向量，嵌入的参数能够随着模型一起学习。注意，嵌入权重还多乘了一个\(\sqrt{d_{model}}\)。

位置编码是整个Transformer中最无厘头的一部分，选用的方法非常奇怪。位置编码使用相同形状的位置嵌入矩阵\(\mathbf{P}\)，矩阵\(\mathbf{P}\)的值满足以下关系式：

偶数列： \[ P_{i,2j}=sin(\frac{i}{10000^{2j/d}}) \] 奇数列： \[ P_{i,2j+1}=cos(\frac{i}{10000^{2j/d}}) \]

实现一个Transformer Encoder

1
2
3
4
5
6
7
8
9
10
11
class AttentionEncoderBlock(nn.Module):
    def __init__(self, num_hiddens, num_heads, dropout_rate, ffn_hiddens, USEBIAS):
        super().__init__()
        self.attention = Multi_Atttention(num_hiddens, num_heads, dropout_rate, USEBIAS)
        self.addNorm1 = Add_Norm(num_hiddens, dropout_rate)
        self.ffn = PositionWiseFFN(ffn_hiddens, num_hiddens)
        self.addNorm2 = Add_Norm(num_hiddens, dropout_rate)

    def forward(self, X, valid_lens):
        Y = self.addNorm1(X, self.attention(X, X, X, valid_lens))
        return self.addNorm2(Y, self.ffn(Y))

BERT架构

从Transformer到BERT

  1. BERT Encoder Block的形状与Transformer Encoder Block的主体结构相同，因此可以直接复用
  2. BERT位置编码通过构建随机初始化的参数矩阵通过学习得到
  3. 由于BERT的输入不是单个的句子而是句子对，为了区分是前一个句子还是后一个句子，引入了段落编码
实现BERTEncoder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class BERTEncoder(nn.Module):
    def __init__(self, vocab_size, num_hiddens, num_heads, dropout_rate, ffn_hiddens, num_blks, max_len, bias, **kwargs):
        super(BERTEncoder, self).__init__(**kwargs)
        self.token_embedding = nn.Embedding(vocab_size, num_hiddens)
        self.segments_embedding = nn.Embedding(2, num_hiddens)
        self.blks = nn.Sequential()
        for _ in range(num_blks):
            self.blks.add_module(f"TransformerEncoder{_}", AttentionEncoderBlock(
                num_hiddens, num_heads, dropout_rate, ffn_hiddens, USEBIAS=bias))
        self.pos_embedding = nn.Parameter(torch.randn(1, max_len, num_hiddens))

    def forward(self, tokens, segments, valid_lens):
        X = self.token_embedding(tokens) + self.segments_embedding(segments)
        X += self.pos_embedding[:, :X.shape[1], :]
        for blk in self.blks:
            X = blk(X, valid_lens)
        return X

自监督

BERT通过两个任务实现了自监督学习

任务一：预测被随机<mask>的词（完形填空）
  • 本质上是一个多分类的任务
  • 根据经过BERTEncoder的输出，取出需要预测的词所在位置的特征表示（认为这个位置包含了词本身的性质以及与其他词关系的所有信息）
  • 将拿到的特征表示作为一个MLP的输入，分类到词表大小
代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class PredMaskedToken(nn.Module):
        def __init__(self, num_hiddens, vocab_size, **kwargs):
        super(PredMaskedToken, self).__init__(**kwargs)
        self.classifier = nn.Sequential(nn.LazyLinear(num_hiddens),
                                 nn.ReLU(),
                                 nn.LayerNorm(num_hiddens),
                                 nn.LazyLinear(vocab_size))

    def forward(self,X, pred_position):
        batch_size, num_preds = X.shape[0], pred_position.shape[1]
        batch_index = torch.repeat_interleave(torch.arange(0,  batch_size), num_preds)
        masked_X = X[batch_index, pred_position.reshape(-1)]
        masked_X = torch.reshape(masked_X, (batch_size, num_preds, -1))
        return self.classifier(masked_X)

pred_position的形状为(batch_size, num_preds)，每一个批量中的内容都是需要预测的词的位置索引

为了获取索引信息，这里使用了PyTorch的高级索引技巧

首先输入X的形状为(batch_size, len_sentencePairs, num_hiddens)，X包含了每个批量中每个字符的所有特征维度的信息

现在，我们的目标是索引出每个批量需要预测的字符的所有特征维的信息

按照常规的思路，索引其中一个批量的一个字符的特征，会使用X[(batch_index, one_predPos)]

  • 例如：

    1
    X = torch.randn((2,4,5))

    1
    2
    3
    4
    5
    6
    7
    8
    9
    tensor([[[-0.4885,  0.0097, -2.4597,  0.1487,  1.4205],
             [ 0.9140,  0.5731,  1.1893,  0.8911, -1.8921],
             [ 1.1929, -1.0281,  0.3921, -0.1117, -1.0114],
             [-0.2798, -0.3925, -0.1226, -1.3862, -1.7268]],

            [[ 0.1964, -0.3935,  1.1851, -0.8282, -1.5966],
             [ 0.3506, -1.4511,  0.1969,  0.9041,  0.8857],
             [ 1.4290, -0.1206,  1.9447, -1.9729,  0.6238],
             [ 0.6116, -0.6430, -0.9231,  0.1967, -0.4616]]])

    • 索引一个字符：

      1
      X[0, 1] # -> 第0个批量第1个字符的所有特征

      1
      tensor([ 0.9140,  0.5731,  1.1893,  0.8911, -1.8921])

    • 索引来自不同批量的多个字符

      1
      X[(0, 0, 1, 1), (0, 1, 2, 3)]

      1
      2
      3
      4
      tensor([[-0.4885,  0.0097, -2.4597,  0.1487,  1.4205],
              [ 0.9140,  0.5731,  1.1893,  0.8911, -1.8921],
              [ 1.4290, -0.1206,  1.9447, -1.9729,  0.6238],
              [ 0.6116, -0.6430, -0.9231,  0.1967, -0.4616]])

      观察发现，每一个索引的效果其实等效于用来索引两个参数对应位置组合来实现的 ->输出的第0行就是X[(0, 0)]

根据这个提示，于是就有了一种思路：

  • 既然索引的第一个参数用来指定批量索引，那么可以创建一个有arange一个batch_size长的张量，然后内部复制num_preds次

  • 第二个元素是表示再每一个批量的位置，既然有了批量位置的定位，这部分就只用把pred_position展开成一个一维的张量

  • 故有了这样的写法：

    1
    2
    batch_index = torch.repeat_interleave(torch.arange(0, batch_size), num_preds)
    masked_X = X[batch_index, pred_position.reshape(-1)]

PyTorch的Linear操作的是最后一个维度，因此，h还需要将masked_X恢复成最初的形状

1
masked_X = torch.reshape(masked_X, (batch_size, num_preds, -1))
任务二：预测句子对中的句子第二个句子是不是相邻的句子
  • 为了实现这个功能在句子对的开头添加了<cls>的标签，这个标签专门用来进行是不是下一个句子的预测
  • 预测的本质实际上是一个二分类问题，<cls>标签跟随句子通过BERTEncoder后的输出可以认为包含了整个句子的信息
代码实现：
1
2
3
4
5
6
7
8
9
10
class PreNextSentence(nn.Module):
    def __init__(self, num_hiddens, **kwargs):
        super(PreNextSentence, self).__init__(**kwargs)
        self.output = nn.LazyLinear(2)
        self.hidden = nn.Sequential(nn.LazyLinear(num_hiddens),
                                    nn.Tanh())

    def forward(self, X):
        X = self.hidden(X[:, 0, :])  # PyTorch能自动去掉长度为1的维度，故：X.shape=(batch_size, num_hiddens)
        return self.output(X)

实现BERTModel

这部分就是连接自监督的两个任务

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class BERTModel(nn.Module):
    def __init__(self, vocab_size, num_hiddens, num_heads, dropout_rate, ffn_hiddens, num_blks, max_len=1000, bias=False, **kwargs):
        super(BERTModel, self).__init__(**kwargs)
        self.encoder = BERTEncoder(vocab_size, num_hiddens, num_heads, dropout_rate, ffn_hiddens, num_blks, max_len, bias, **kwargs)
        self.mlm = PredMaskedToken(num_hiddens, vocab_size)
        self.pns = PreNextSentence(num_hiddens)

    def forward(self, tokens, segments, valid_lens=None, pred_position=None):
        encoded_X = self.encoder(tokens, segments, valid_lens)
        if pred_position is not None:
            mlm_hat = self.mlm(encoded_X, pred_position)
        else:
            mlm_hat = None
        pns_hat = self.pns(encoded_X)
        return encoded_X, mlm_hat, pns_hat

PreTraining

Dataset

要进行训练，先要构建一个用于BERT训练的数据集，在d2l的Demo中，演示使用构建了一个简单的数据集，但这部分代码不容易理解，这部分尝试从一个初学者的角度尝试构建数据集

回忆数据集需要包含的内容

  • BERT的数据集是一个句子对，句子对会被填充或截断到相同的长度max_len，返回包含和句子对相同形状的valid_lens，需要返回用于segment编码的序列（第一个句子对应的字符的标签为0，第2个句子为1）
  • 数据集能够完成两个自监督任务
    • 数据集中的句子对中的部分词被Mask掉，返回的数据集需要包含Masked的句子对表示，Masked的词位置，Mask前的词索引表示
    • 一部分句子的第二句被替换掉，为了能够预测句子对的开头需要加上<cls>标签，每一句的末尾需要加上<seq>标签，返回是否有被替换的结果标签（包含True & False）以及替换后的句子对

分析任务流的先后顺序可以这样实现：

从磁盘读取数据集\(\longrightarrow\)构建字典（包含可能用到的特殊标签）\(\longrightarrow\)生成句子对\(\longrightarrow\)添加开头、句末的标签\(\longrightarrow\)随机句子替换\(\longrightarrow\)随机字符掩蔽\(\longrightarrow\)根据字符生成索引\(\longrightarrow\)填充到max_len\(\longrightarrow\)生成用于segment编码的序列

代码实现

导入依赖包：

1
2
3
4
5
6
7
import collections
import random
import pandas as pd
from torch import tensor
from torch import float32, long
from torch import save
import torch.utils.data as data
读取数据集

下载wikitext2的训练数据集.parquet格式用于导入

1
2
3
4
5
6
7
8
9
10
11
def read_data_from_parquet(data_path):
    """
    从磁盘读取数据文件
    文件格式为: <.parquet>
    """
    df = pd.read_parquet(data_path)
    lines = df['text'].tolist()
    paragraphs = [line.strip().lower().split(' . ')
                  for line in lines if len(line.split(' . ')) >= 2]
    random.shuffle(paragraphs)
    return paragraphs
构建字典

在原版BERT中使用的是词根的方法，这里做简化处理

字典设置一个字符出现的最小频率（小于该频率的用<unk>表示减小字典大小），实现索引到字词idx_to_token和字词到索引token_to_idx两个方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Vocab:
    """
    两个方法：
    idx_to_tokens: 根据索引查单词
    tokens_to_idx: 根据单词查索引
    包含保留字符
    len()方法返回的长度不包含保留字符
    """

    def __init__(self, all_paragraphs, min_freq):
        _tokens = [token for paragraph in all_paragraphs for sentence in paragraph for token in sentence.split(' ')]
        self.counter = limit_min_freq(collections.Counter(_tokens), min_freq)
        self.idx_to_token_dict = {0: '<mask>', 1: '<cls>', 2: '<sep>', 3: '<pad>', 4: '<unk>'}
        for i, token in enumerate(self.counter.keys()):
            self.idx_to_token_dict[i+5] = token
        self.token_to_idx_dict = {'<mask>': 0, '<cls>': 1, '<sep>': 2, '<pad>': 3, '<unk>': 4}
        for i, token in enumerate(self.counter.keys()):
            self.token_to_idx_dict[token] = i+5


    @property
    def list_vocab(self):
        return list(self.counter.keys())

    @property
    def get_state(self):
        return {
            "token_to_idx": self.token_to_idx_dict,
            "idx_to_token": self.idx_to_token_dict,
        }

    def idx_to_token(self, index):
        return self.idx_to_token_dict[index]

    def token_to_idx(self, token):
        try:
            index = self.token_to_idx_dict[token]
        except:
            index = 4
        return index

    def __len__(self):
        return len(self.counter)
    
    
def limit_min_freq(counter, min_freq):
    for token, freq in list(counter.items()):
        if freq < min_freq:
            del counter[token]
    return counter
生成随机替换掉的句子对

有50%的概率第二句话被替换为随机选取的句子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 输入两个句子生成句子对并添加标签，有50%的概率被替换
def generate_sentence_pair(sentence_a: str, sentence_b: str, paragraphs=None, require_next_pred=False):
    sentence_a = sentence_a.split(' ')
    sentence_b = sentence_b.split(' ')
    _temp = ['<cls>'] + sentence_a + ['<sep>']
    isNext = True
    if require_next_pred:
        try:
            random_sentence = random.choice(random.choice(paragraphs))
            isinstance(random_sentence, str)
            if random.random() < 0.5:
                sentence_b = random_sentence.split(' ')
                isNext = False
        except:
            raise ParagraphsError
    _temp = _temp + sentence_b + ['<sep>']
    _segment = [0] * (len(sentence_a) + 2) + [1] * (len(sentence_b) + 1)
    return (_temp, _segment, isNext)


class ParagraphsError(Exception):
    def __init__(self):
        print("Check Paragraphs")
        

# 生成一段话的Pred_Next_Sentence数据的方法
def get_pns_data_each_para(paragraph, paragraphs, max_len):
    """
    返回: [tuple1, tuple2, ...]
    tuple[0]: sentence_pair -> list，包含句子对按' '的分词
    tuple[1]: segment -> list value: 0 or 1; length: len(sentence_pair)
    tuple[2]: isNext -> boolean True: 第二个句子没有被替换
                                False: 第二个句子被替换
    """
    sentence_pair = []
    for i in range(len(paragraph) - 1):
        _temp = generate_sentence_pair(paragraph[i], paragraph[i + 1], paragraphs, require_next_pred=True)
        if len(_temp[0]) <= max_len:
            sentence_pair.append(_temp)
    return sentence_pair
随机掩蔽单词

有句子对长度，15%的单词被掩蔽

掩蔽有三种方法完成

  1. 80%概率将单词置为特殊标签<mask>；
  2. 10%概率随机选一个词替换；
  3. 10%概率保持不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 实现替换词的方法
def replace_token(sentence_pair, candidate_position, vocab):
    max_index = len(vocab) + 4  # len(vocab)+5-1
    random.shuffle(candidate_position)
    max_masked_token = round(len(sentence_pair) * 0.15)
    masked_token = {}
    for i in candidate_position:
        if len(masked_token) > max_masked_token:
            break
        if random.random() < 0.8:
            mask = '<mask>'
        else:
            if random.random() < 0.5:
                mask = vocab.idx_to_token(random.randint(5, max_index))
            else:
                mask = sentence_pair[i]
        masked_token.update({i: vocab.token_to_idx(sentence_pair[i])})
        sentence_pair[i] = mask
    return (sentence_pair, masked_token)


def get_masked_tokens_data(pair_list, vocab):
    """
    返回：
    类型：list, list的元素类型为tuple
    每个tuple对应一个句子对
    tuple[0] -> sentence_pair -> list
    tuple[1] -> masked_tokens -> dict
                                    dict.keys(): 需要预测的（被replace掉的）词的位置
                                    dict.values(): 被replace之前的词
    """
    masked_tokens_data = []
    for pair_tuple in pair_list:
        candidate_pos = []
        sentence_pair = pair_tuple[0]  # pair_tuple: tuple
        for i, token in enumerate(sentence_pair):
            if token in ['cls', 'sep']:
                continue
            candidate_pos.append(i)
        masked_sentence_pair_and_token = replace_token(sentence_pair, candidate_pos, vocab)
        masked_tokens_data.append(masked_sentence_pair_and_token)
    return masked_tokens_data

生成每一段的数据集（数据样本的结构：数据集->段->句子）

1
2
3
4
5
6
7
8
9
def loadEachDate(paragraph, paragraphs, vocab, max_len=1000):
    """
    合并方法get_pns_data_all_paras和方法get_masked_tokens_data
    返回：
    data_for_pns, data_for_mlm
    """
    data_for_pns = get_pns_data_each_para(paragraph, paragraphs, max_len)
    data_for_mlm = get_masked_tokens_data(data_for_pns, vocab)
    return data_for_pns, data_for_mlm
填充并生成索引

这里的填充不仅包括句子对的填充，由于句子对的长度不同，导致mask的长度也不同，故也需要填充，而为了区分哪些是填充，哪些是真实的<mask>标签，引入了masked_weights(具体用法将在实现训练部分说明)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def to_idx(sentence, vocab):
    return [vocab.token_to_idx(token) for token in sentence]


def idx_padding_data(max_len, vocab, sentence_pair, segment, maksed_pos, masked_token):
    valid_len = len(sentence_pair)
    padding_for_sentencePair = ['<pad>']*(max_len-valid_len)
    padding_for_segment = [0]*(max_len-len(segment))
    _padding_mask_length = round(max_len*0.15) - len(maksed_pos)
    masked_weights = [1]*len(maksed_pos)+[0]*_padding_mask_length
    padding_for_pos = [0]*(_padding_mask_length)
    padding_for_maskedToken = ['<pad>']*(_padding_mask_length)
    sentence_pair = to_idx(sentence_pair+padding_for_sentencePair, vocab)
    segment = segment+padding_for_segment
    maksed_pos = maksed_pos+padding_for_pos
    masked_token = to_idx(masked_token+padding_for_maskedToken, vocab)
    return sentence_pair, segment, valid_len, maksed_pos, masked_token, masked_weights
构建数据集

使用PyTorch构建数据集采用实现torch.utils.data中的Dataset来实现

查看PyTorch中的Dataset部分的源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Dataset(Generic[T_co]):
    r"""An abstract class representing a :class:`Dataset`.

    All datasets that represent a map from keys to data samples should subclass
    it. All subclasses should overwrite :meth:`__getitem__`, supporting fetching a
    data sample for a given key. Subclasses could also optionally overwrite
    :meth:`__len__`, which is expected to return the size of the dataset by many
    :class:`~torch.utils.data.Sampler` implementations and the default options
    of :class:`~torch.utils.data.DataLoader`.

    .. note::
      :class:`~torch.utils.data.DataLoader` by default constructs a index
      sampler that yields integral indices.  To make it work with a map-style
      dataset with non-integral indices/keys, a custom sampler must be provided.
    """

    def __getitem__(self, index) -> T_co:
        raise NotImplementedError

    def __add__(self, other: 'Dataset[T_co]') -> 'ConcatDataset[T_co]':
        return ConcatDataset([self, other])
  • Dataset是一个抽象类，继承这个抽象类的时候必须实现__getitem__接口，这个接口接受输入为索引值，根据索引值返回对应批量的标签。
  • 此外Dataset还实现了一个__add__方法，用来用来将两个数据集合并
  • 从注释中可以知道，Dataset搭配DataLoader使用

实现：

这里额外实现一个save方法，用来保存数据集，方便下次调用，Vocab将以JSON的格式保存

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class LoadBERTData(data.Dataset):
    def __init__(self, data_path, max_len, min_freq, **kwargs):
        super(LoadBERTData, self).__init__(**kwargs)
        paragraphs = read_data_from_parquet(data_path)
        self.vocab = Vocab(paragraphs, min_freq)
        self.sentence_pairs, self.segments, self.valid_lens,  self.masked_pos, self.masked_tokens, self.masked_wights, self.nextSentenceLabel,= [], [], [], [], [], [], []
        for example in paragraphs:
            data_for_pns, data_for_mlm = loadEachDate(example, paragraphs, self.vocab, max_len)
            for _ in data_for_pns:
                self.segments.append(_[1])
                self.nextSentenceLabel.append(_[2])
            for _ in data_for_mlm:
                self.sentence_pairs.append(_[0])
                self.masked_pos.append(list(_[1].keys()))
                self.masked_tokens.append(list(_[1].values()))
        for i, zip_input in enumerate(zip(self.sentence_pairs, self.segments, self.masked_pos, self.masked_tokens)):
            self.sentence_pairs[i], self.segments[i], valid_lens, self.masked_pos[i], self.masked_tokens[i], masked_weights = idx_padding_data(max_len, self.vocab, *zip_input)
            self.valid_lens.append(valid_lens)
            self.masked_wights.append(masked_weights)
        self.sentence_pairs = tensor(self.sentence_pairs, dtype=long)
        self.segments = tensor(self.segments, dtype=long)
        self.valid_lens = tensor(self.segments, dtype=float32)
        self.masked_pos = tensor(self.masked_pos, dtype=long)
        self.masked_wights = tensor(self.masked_wights, dtype=float32)
        self.masked_tokens = tensor(self.masked_tokens, dtype=long)
        self.nextSentenceLabel = tensor(self.nextSentenceLabel, dtype=long)

    def __getitem__(self, idx):
        return (self.sentence_pairs[idx], self.segments[idx], self.valid_lens[idx],
                self.masked_pos[idx], self.masked_wights[idx],
                self.masked_tokens[idx], self.nextSentenceLabel[idx])

    def __len__(self):
        return len(self.sentence_pairs)

    def save(self, vocabPath=None, ptPath=None):
        if vocabPath is not None:
            _vocab = {
                "idx2token": self.vocab.idx_to_token_dict,
                "token2idx": self.vocab.idx_to_token_dict}
            with open(vocabPath, 'w') as myJSON:
                json.dump(_vocab, myJSON)
        if ptPath is not None:
            dataset = {
                'sentence_pairs': self.sentence_pairs,
                'segments': self.segments,
                'valid_lens': self.valid_lens,
                'masked_pos': self.masked_pos,
                'masked_wights': self.masked_wights,
                'masked_tokens': self.masked_tokens,
                'nextSentenceLabel': self.nextSentenceLabel,
            }
            save(dataset, ptPath)
1
2
3
def generateDateset(Dateset, batchsize):
    train_iter = data.DataLoader(Dateset, batchsize)
    return train_iter
生成训练集
1
2
3
4
5
6
7
8
file_path = "../data/wikitext-2/train.parquet"
dateset = LoadBERTData(file_path, max_len=1000, min_freq=3)
dateset.save("../data/wikitext-2/vocab.json", "../data/wikitext-2/miniWiki.pt")
train_iter = generateDateset(dateset, batchsize=32)
batch = next(iter(train_iter))
sentence_pairs, segments, valid_lens, masked_pos, masked_weights, masked_tokens, nextSentenceLabel = batch
print(sentence_pairs.shape, segments.shape, valid_lens.shape,
      masked_tokens.shape, masked_weights.shape, masked_pos.shape, nextSentenceLabel.shape)

训练

导入数据集：

导入单词表(从JSON)
1
2
3
4
5
6
7
class vocab:
    idx2token = None
    token2idx = None
with open("../data/wikitext-2/vocab.json", 'r') as myVocab:
    temp = json.load(myVocab)
    vocab.idx2token = temp["idx2token"]
    vocab.token2idx = temp["token2idx"]
导入预处理的数据集(从pt)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class dataSet(data.Dataset):
    def __init__(self, ptPath):
        super().__init__()
        dataset = torch.load(ptPath).values()
        self.sentence_pairs, self.segments, self.valid_lens, \
            self.masked_pos, self.masked_wights, \
            self.masked_tokens, self.nextSentenceLabel = dataset
    def __getitem__(self, idx):
        return (self.sentence_pairs[idx], self.segments[idx], self.valid_lens[idx],
                self.masked_pos[idx], self.masked_wights[idx],
                self.masked_tokens[idx], self.nextSentenceLabel[idx])
    def __len__(self):
        return len(self.sentence_pairs)
    

dataset = dataSet("../data/wikitext-2/miniWiki.pt")
trainIter = data.DataLoader(dataset, batch_size=32)

初始化

默认情况下，nn.CrossEntropyLoss中的reduction参数的值为'mean'，会对每个batch中每个预测样本的loss计算一个全局的平均值；

但是，在此次任务中，对于masked_tokens的预测使用到了填充，因此填充部分的损失应该不参与取均值；

因此，这里手动指定reduction='none'，对每个batch的每个预测不做处理

1
2
3
4
5
devices = torch.device("cuda" if torch.cuda.is_available() else "cpu")
loss = nn.CrossEntropyLoss(reduction='none')
num_steps, learning_rate = 50, 0.01
loss_mlm, loss_pns, loss_add = [], [], []
myBERT = BERTModel(vocab_size=len(vocab.idx2token), num_hiddens=32, num_heads=4, dropout_rate=0.3, ffn_hiddens=64, num_blks=2, max_len=1000, bias=True)

计算每一个step的损失

在生成maked_tokens的数据集中引入了一个标记masked_weights，真实的预测位置标记为1，填充部分的标记为0，这里计算均值时使用所有loss的和去除以真实位置的数量

1
2
3
4
5
6
7
8
9
10
11
def getBatchLoss(net, loss,
                 sentence_pairs, segments, valid_lens,
                 masked_pos, masked_weights,
                 masked_tokens, nextSentenceLabel):
    encoded_X, mlm_hat, pns_hat = net(sentence_pairs, segments, valid_lens, masked_pos)
    mlm_l = loss(mlm_hat.reshape(-1, mlm_hat.size(-1)), masked_tokens.reshape(-1))
    mlm_l = mlm_l.sum() / (masked_weights.sum() + 1e-8)
    pns_l = loss(pns_hat, nextSentenceLabel)
    pns_l = pns_l.mean()
    l = mlm_l + pns_l
    return mlm_l, pns_l, l

训练BERT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def trainBert(train_iter, net, loss, device, num_steps, lr=learning_rate):
    net(*next(iter(train_iter))[:4])
    net = net.to(device)
    trainer = torch.optim.Adam(net.parameters(), lr=lr)
    step = 0
    while step < num_steps:
        for sentence_pairs, segments, valid_lens, \
                masked_pos, masked_weights, \
                masked_tokens, nextSentenceLabel in train_iter:
            sentence_pairs = sentence_pairs.to(device)
            segments = segments.to(device)
            valid_lens = valid_lens.to(device)
            masked_pos = masked_pos.to(device)
            masked_weights = masked_weights.to(device)
            masked_tokens = masked_tokens.to(device)
            nextSentenceLabel = nextSentenceLabel.to(device)
            trainer.zero_grad()
            start_time = time.time()
            mlm_l, pns_l, l = getBatchLoss(net, loss,
                                           sentence_pairs, segments, valid_lens,
                                           masked_pos, masked_weights,
                                           masked_tokens, nextSentenceLabel)
            l.backward()
            trainer.step()
            end_time = time.time()
            TimeUse = end_time-start_time
            print(f"num_steps {step+1}: \n"
                  f"mlm_l: {mlm_l}; \n"
                  f"pns_l: {pns_l}; \n"
                  f"loss: {l}; \n"
                  f"time: {TimeUse}. \n"
                  f"====================================================")
            loss_mlm.append(mlm_l.detach().numpy())
            loss_pns.append(pns_l.detach().numpy())
            loss_add.append(l.detach().numpy())
            step += 1
            if step == num_steps:
                break

展示

这里只展示代码能够正常运行，实际上，在真实的BERT预训练与d2l课程中的Demo有较大的差距

Model / Params num_hiddens ffn_hiddens num_heads
BERT base 768 3072 12
BERT large 1024 4096 16

此外，BERT中的激活函数用的是GeLu而不是ReLu

  • ReLu: \[ f(x) = max(0, x) \]

  • GeLu: \[ f(x) = x \cdot \Phi(x) \]

    \[ \Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x} e^{-\frac{t^2}{2}} d \]

  • 对比

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    import numpy as np
    import matplotlib.pyplot as plt

    # 定义 ReLU 函数
    def relu(x):
        return np.maximum(x, 0)

    # 定义 GELU 函数
    def gelu(x):
        return x * 0.5 * (1.0 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3))))

    # 生成 -3 ～ 3 的连续数字作为 x 坐标
    x = np.linspace(-3, 3, 1000)

    # 绘制图像
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
    fig.suptitle('Comparison of ReLU and GELU Functions')

    # 在子图 1 中绘制 ReLU 函数
    ax1.plot(x, relu(x), label='ReLU', lw=2)
    ax1.set_ylim([-0.5, 3])
    ax1.axhline(y=0, color='k', lw=0.5)
    ax1.axvline(x=0, color='k', lw=0.5)
    ax1.set_xlabel('x')
    ax1.set_ylabel('ReLU(x)')
    ax1.legend()

    # 在子图 2 中绘制 GELU 函数
    ax2.plot(x, gelu(x), label='GELU', lw=2)
    ax2.set_ylim([-0.5, 3])
    ax2.axhline(y=0, color='k', lw=0.5)
    ax2.axvline(x=0, color='k', lw=0.5)
    ax2.set_xlabel('x')
    ax2.set_ylabel('GELU(x)')
    ax2.legend()

    # 显示图形
    plt.show()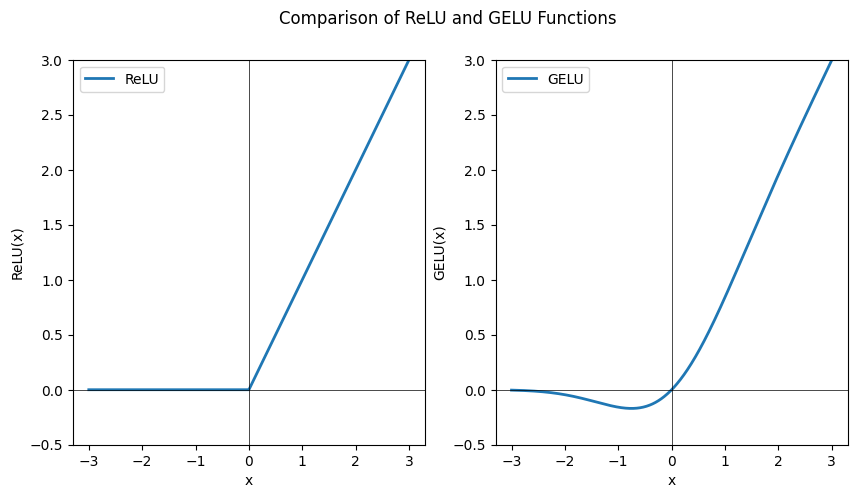

    relu-gelu

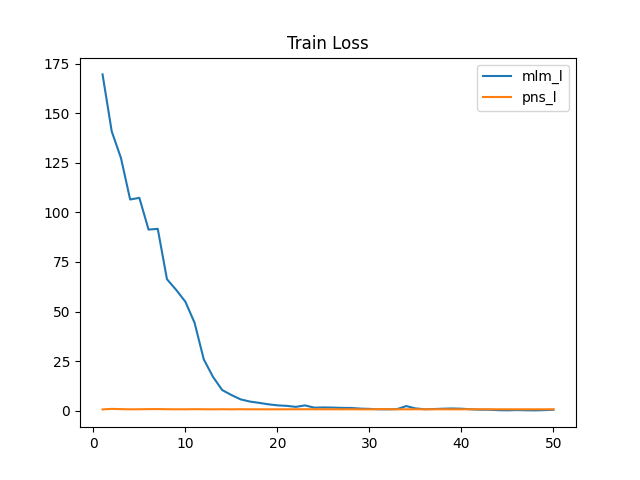
第一轮结束：

1
2
3
4
num_steps 1: 
mlm_l: 169.5784454345703; 
pns_l: 0.630012035369873; 
loss: 170.2084503173828;

按照上面的参数，50轮训练后

1
2
3
4
num_steps 50: 
mlm_l: 0.4629861116409302; 
pns_l: 0.6946119070053101; 
loss: 1.1575980186462402;
result

关于预训练部分的代码汇总

数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
import collections
import random
import pandas as pd
from torch import tensor
from torch import float32, long
from torch import save
import torch.utils.data as data
import json


def generateDateset(Dateset, batchsize):
    train_iter = data.DataLoader(Dateset, batchsize)
    return train_iter


class LoadBERTData(data.Dataset):
    def __init__(self, data_path, max_len, min_freq, **kwargs):
        super(LoadBERTData, self).__init__(**kwargs)
        paragraphs = read_data_from_parquet(data_path)
        self.vocab = Vocab(paragraphs, min_freq)
        self.sentence_pairs, self.segments, self.valid_lens,  self.masked_pos, self.masked_tokens, self.masked_wights, self.nextSentenceLabel,= [], [], [], [], [], [], []
        for example in paragraphs:
            data_for_pns, data_for_mlm = loadEachDate(example, paragraphs, self.vocab, max_len)
            for _ in data_for_pns:
                self.segments.append(_[1])
                self.nextSentenceLabel.append(_[2])
            for _ in data_for_mlm:
                self.sentence_pairs.append(_[0])
                self.masked_pos.append(list(_[1].keys()))
                self.masked_tokens.append(list(_[1].values()))
        for i, zip_input in enumerate(zip(self.sentence_pairs, self.segments, self.masked_pos, self.masked_tokens)):
            self.sentence_pairs[i], self.segments[i], valid_lens, self.masked_pos[i], self.masked_tokens[i], masked_weights = idx_padding_data(max_len, self.vocab, *zip_input)
            self.valid_lens.append(valid_lens)
            self.masked_wights.append(masked_weights)
        self.sentence_pairs = tensor(self.sentence_pairs, dtype=long)
        self.segments = tensor(self.segments, dtype=long)
        self.valid_lens = tensor(self.segments, dtype=float32)
        self.masked_pos = tensor(self.masked_pos, dtype=long)
        self.masked_wights = tensor(self.masked_wights, dtype=float32)
        self.masked_tokens = tensor(self.masked_tokens, dtype=long)
        self.nextSentenceLabel = tensor(self.nextSentenceLabel, dtype=long)

    def __getitem__(self, idx):
        return (self.sentence_pairs[idx], self.segments[idx], self.valid_lens[idx],
                self.masked_pos[idx], self.masked_wights[idx],
                self.masked_tokens[idx], self.nextSentenceLabel[idx])

    def __len__(self):
        return len(self.sentence_pairs)

    def save(self, vocabPath=None, ptPath=None):
        if vocabPath is not None:
            _vocab = {
                "idx2token": self.vocab.idx_to_token_dict,
                "token2idx": self.vocab.idx_to_token_dict}
            with open(vocabPath, 'w') as myJSON:
                json.dump(_vocab, myJSON)
        if ptPath is not None:
            dataset = {
                'sentence_pairs': self.sentence_pairs,
                'segments': self.segments,
                'valid_lens': self.valid_lens,
                'masked_pos': self.masked_pos,
                'masked_wights': self.masked_wights,
                'masked_tokens': self.masked_tokens,
                'nextSentenceLabel': self.nextSentenceLabel,
            }
            save(dataset, ptPath)


def read_data_from_parquet(data_path):
    """
    从磁盘读取数据文件
    文件格式为: <.parquet>
    """
    df = pd.read_parquet(data_path)
    lines = df['text'].tolist()
    paragraphs = [line.strip().lower().split(' . ')
                  for line in lines if len(line.split(' . ')) >= 2]
    random.shuffle(paragraphs)
    return paragraphs


def loadEachDate(paragraph, paragraphs, vocab, max_len=1000):
    """
    合并方法get_pns_data_all_paras和方法get_masked_tokens_data
    返回：
    data_for_pns, data_for_mlm
    """
    data_for_pns = get_pns_data_each_para(paragraph, paragraphs, max_len)
    data_for_mlm = get_masked_tokens_data(data_for_pns, vocab)
    return data_for_pns, data_for_mlm


def get_masked_tokens_data(pair_list, vocab):
    """
    生成“完型填空”的数据
    allSentencePairs:
    内容：所有的未masked的句子对
    类型：列表，列表的每个元素是元组，元组的第一个值才是sentence_pair分词的列表
    返回：
    类型：list, list的元素类型为tuple
    每个tuple对应一个句子对
    tuple[0] -> sentence_pair -> list
    tuple[1] -> masked_tokens -> dict
                                    dict.keys(): 需要预测的（被replace掉的）词的位置
                                    dict.values(): 被replace之前的词
    """
    masked_tokens_data = []
    for pair_tuple in pair_list:
        candidate_pos = []
        sentence_pair = pair_tuple[0]  # pair_tuple: tuple
        for i, token in enumerate(sentence_pair):
            if token in ['cls', 'sep']:
                continue
            candidate_pos.append(i)
        masked_sentence_pair_and_token = replace_token(sentence_pair, candidate_pos, vocab)
        masked_tokens_data.append(masked_sentence_pair_and_token)
    return masked_tokens_data


def idx_padding_data(max_len, vocab, sentence_pair, segment, maksed_pos, masked_token):
    valid_len = len(sentence_pair)
    padding_for_sentencePair = ['<pad>']*(max_len-valid_len)
    padding_for_segment = [0]*(max_len-len(segment))
    _padding_mask_length = round(max_len*0.15) - len(maksed_pos)
    masked_weights = [1]*len(maksed_pos)+[0]*_padding_mask_length
    padding_for_pos = [0]*(_padding_mask_length)
    padding_for_maskedToken = ['<pad>']*(_padding_mask_length)
    sentence_pair = to_idx(sentence_pair+padding_for_sentencePair, vocab)
    segment = segment+padding_for_segment
    maksed_pos = maksed_pos+padding_for_pos
    masked_token = to_idx(masked_token+padding_for_maskedToken, vocab)
    return sentence_pair, segment, valid_len, maksed_pos, masked_token, masked_weights


def replace_token(sentence_pair, candidate_position, vocab):
    max_index = len(vocab) + 4  # len(vocab)+5-1
    random.shuffle(candidate_position)
    max_masked_token = round(len(sentence_pair) * 0.15)
    masked_token = {}
    for i in candidate_position:
        if len(masked_token) > max_masked_token:
            break
        if random.random() < 0.8:
            mask = '<mask>'
        else:
            if random.random() < 0.5:
                mask = vocab.idx_to_token(random.randint(5, max_index))
            else:
                mask = sentence_pair[i]
        masked_token.update({i: vocab.token_to_idx(sentence_pair[i])})
        sentence_pair[i] = mask
    return (sentence_pair, masked_token)


def get_pns_data_each_para(paragraph, paragraphs, max_len):
    """
    返回: [tuple1, tuple2, ...]
    tuple[0]: sentence_pair -> list，包含句子对按' '的分词
    tuple[1]: segment -> list value: 0 or 1; length: len(sentence_pair)
    tuple[2]: isNext -> boolean True: 第二个句子没有被替换
                                False: 第二个句子被替换
    """
    sentence_pair = []
    for i in range(len(paragraph) - 1):
        _temp = generate_sentence_pair(paragraph[i], paragraph[i + 1], paragraphs, require_next_pred=True)
        if len(_temp[0]) <= max_len:
            sentence_pair.append(_temp)
    return sentence_pair


class Vocab:
    """
    两个方法：
    idx_to_tokens: 根据索引查单词
    tokens_to_idx: 根据单词查索引
    保留字符
    len()方法返回的长度不包含保留字符
    """

    def __init__(self, all_paragraphs, min_freq):
        _tokens = [token for paragraph in all_paragraphs for sentence in paragraph for token in sentence.split(' ')]
        self.counter = limit_min_freq(collections.Counter(_tokens), min_freq)
        self.idx_to_token_dict = {0: '<mask>', 1: '<cls>', 2: '<sep>', 3: '<pad>', 4: '<unk>'}
        for i, token in enumerate(self.counter.keys()):
            self.idx_to_token_dict[i+5] = token
        self.token_to_idx_dict = {'<mask>': 0, '<cls>': 1, '<sep>': 2, '<pad>': 3, '<unk>': 4}
        for i, token in enumerate(self.counter.keys()):
            self.token_to_idx_dict[token] = i+5

    @property
    def list_vocab(self):
        return list(self.counter.keys())

    @property
    def get_state(self):
        return {
            "token_to_idx": self.token_to_idx_dict,
            "idx_to_token": self.idx_to_token_dict,
        }

    def idx_to_token(self, index):
        return self.idx_to_token_dict[index]

    def token_to_idx(self, token):
        try:
            index = self.token_to_idx_dict[token]
        except:
            index = 4
        return index

    def __len__(self):
        return len(self.counter)

def limit_min_freq(counter, min_freq):
    for token, freq in list(counter.items()):
        if freq < min_freq:
            del counter[token]
    return counter


def generate_sentence_pair(sentence_a: str, sentence_b: str, paragraphs=None, require_next_pred=False):
    sentence_a = sentence_a.split(' ')
    sentence_b = sentence_b.split(' ')
    _temp = ['<cls>'] + sentence_a + ['<sep>']
    isNext = True
    if require_next_pred:
        try:
            random_sentence = random.choice(random.choice(paragraphs))
            isinstance(random_sentence, str)
            if random.random() < 0.5:
                sentence_b = random_sentence.split(' ')
                isNext = False
        except:
            raise ParagraphsError
    _temp = _temp + sentence_b + ['<sep>']
    _segment = [0] * (len(sentence_a) + 2) + [1] * (len(sentence_b) + 1)
    return (_temp, _segment, isNext)


def to_idx(sentence, vocab):
    return [vocab.token_to_idx(token) for token in sentence]


class ParagraphsError(Exception):
    def __init__(self):
        print("Check Paragraphs")


if __name__ == '__main__':
    file_path = "../data/wikitext-2/train.parquet"
    dateset = LoadBERTData(file_path, max_len=1000, min_freq=3)
    dateset.save("../data/wikitext-2/vocab.json", "../data/wikitext-2/miniWiki.pt")
    train_iter = generateDateset(dateset, batchsize=32)
    batch = next(iter(train_iter))
    sentence_pairs, segments, valid_lens, masked_pos, masked_weights, masked_tokens, nextSentenceLabel = batch
    print(sentence_pairs.shape, segments.shape, valid_lens.shape,
          masked_tokens.shape, masked_weights.shape, masked_pos.shape, nextSentenceLabel.shape)

预训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
import math
import time
import json
import matplotlib.pyplot as plt
import torch.utils.data as data
import torch
from torch import nn


class BERTModel(nn.Module):
    def __init__(self, vocab_size, num_hiddens, num_heads, dropout_rate, ffn_hiddens, num_blks, max_len=1000, bias=False, **kwargs):
        super(BERTModel, self).__init__(**kwargs)
        self.encoder = BERTEncoder(vocab_size, num_hiddens, num_heads, dropout_rate, ffn_hiddens, num_blks, max_len, bias, **kwargs)
        self.mlm = PredMaskedToken(num_hiddens, vocab_size)
        self.pns = PreNextSentence(num_hiddens)

    def forward(self, tokens, segments, valid_lens=None, pred_position=None):
        encoded_X = self.encoder(tokens, segments, valid_lens)
        if pred_position is not None:
            mlm_hat = self.mlm(encoded_X, pred_position)
        else:
            mlm_hat = None
        pns_hat = self.pns(encoded_X)
        return encoded_X, mlm_hat, pns_hat


class BERTEncoder(nn.Module):
    '''
    BERTEncoder与Transformer相同，但使用了更多的TransformerEncoderBlock，
    位置编码不再是固定的而是可学习的
    '''
    def __init__(self, vocab_size, num_hiddens, num_heads, dropout_rate, ffn_hiddens, num_blks, max_len, bias, **kwargs):
        super(BERTEncoder, self).__init__(**kwargs)
        self.token_embedding = nn.Embedding(vocab_size, num_hiddens)
        self.segments_embedding = nn.Embedding(2, num_hiddens)
        self.blks = nn.Sequential()
        for _ in range(num_blks):
            self.blks.add_module(f"TransformerEncoder{_}", AttentionEncoderBlock(
                num_hiddens, num_heads, dropout_rate, ffn_hiddens, USEBIAS=bias))
        self.pos_embedding = nn.Parameter(torch.randn(1, max_len, num_hiddens))

    def forward(self, tokens, segments, valid_lens):
        X = self.token_embedding(tokens) + self.segments_embedding(segments)
        X += self.pos_embedding[:, :X.shape[1], :]
        for blk in self.blks:
            X = blk(X, valid_lens)
        return X


class PredMaskedToken(nn.Module):
    '''
    作用：根据上下文预测被masked的词（本质上是一个分类任务）
    参数：
    X：经过BertEncoder的输出
    pre_position：需要预测词的位置
    预测方法：
    索引出X中需要预测词汇的文本信息，形状为(num_preds, embedding_dims)
    传入mlp做分类
    ---索引的方法---
    Example:
    X = torch.rand(2,8,2)
    pre = torch.tensor([[1,5,2],[6,1,5]])
    X[[0,0,0,1,1,1], pre.reshape(-1)]
    [[0,0,0,1,1,1], [1,5,2,6,1,5]]会自动组合索引
    例如，
    第一个[]中的0与第二个[]中的1组合
    传入batch_size为0，第1行，效果等效为X[0,1]，输出为 tensor([0.3709, 0.9237])
    ---
    X:
    tensor([[[0.8112, 0.5804],
         [0.3709, 0.9237],
         [0.2957, 0.9497],
         [0.0212, 0.4065],
         [0.4388, 0.7032],
         [0.0874, 0.5441],
         [0.0384, 0.6714],
         [0.6119, 0.7608]],

        [[0.6988, 0.9494],
         [0.7446, 0.1320],
         [0.7053, 0.0196],
         [0.1830, 0.6116],
         [0.7142, 0.9009],
         [0.0911, 0.2903],
         [0.0724, 0.0587],
         [0.5330, 0.4041]]])
    索引的输出：
    tensor([[0.3709, 0.9237],
            [0.0874, 0.5441],
            [0.2957, 0.9497],
            [0.0724, 0.0587],
            [0.7446, 0.1320],
            [0.0911, 0.2903]])
    '''
    def __init__(self, num_hiddens, vocab_size, **kwargs):
        super(PredMaskedToken, self).__init__(**kwargs)
        self.classifier = nn.Sequential(nn.LazyLinear(num_hiddens),
                                 nn.ReLU(),
                                 nn.LayerNorm(num_hiddens),
                                 nn.LazyLinear(vocab_size))

    def forward(self,X, pred_position):
        batch_size, num_preds = X.shape[0], pred_position.shape[1]
        batch_index = torch.repeat_interleave(torch.arange(0,  batch_size), num_preds)
        masked_X = X[batch_index, pred_position.reshape(-1)]
        masked_X = torch.reshape(masked_X, (batch_size, num_preds, -1))
        return self.classifier(masked_X)


class PreNextSentence(nn.Module):
    '''
    作用：预测两个句子是否相邻
    训练样本：
      在一个句子对中，有50%的概率句子对由相邻的两个句子构成，还有50%的概率下一个句子随机抽取
    构建一个单层的mlp完成预测，判断下一个句子时相邻的还是不是相邻的
    '''
    def __init__(self, num_hiddens, **kwargs):
        super(PreNextSentence, self).__init__(**kwargs)
        self.output = nn.LazyLinear(2)
        self.hidden = nn.Sequential(nn.LazyLinear(num_hiddens),
                                    nn.Tanh())

    def forward(self, X):
        X = self.hidden(X[:, 0, :])
        return self.output(X)


class AttentionEncoderBlock(nn.Module):
    def __init__(self, num_hiddens, num_heads, dropout_rate, ffn_hiddens, USEBIAS):
        super().__init__()
        self.attention = Multi_Atttention(num_hiddens, num_heads, dropout_rate, USEBIAS)
        self.addNorm1 = Add_Norm(num_hiddens, dropout_rate)
        self.ffn = PositionWiseFFN(ffn_hiddens, num_hiddens)
        self.addNorm2 = Add_Norm(num_hiddens, dropout_rate)

    def forward(self, X, valid_lens):
        Y = self.addNorm1(X, self.attention(X, X, X, valid_lens))
        return self.addNorm2(Y, self.ffn(Y))


class Multi_Atttention(nn.Module):
    def __init__(self, num_hiddens,
                 num_heads, dropout_rate, USEBIAS, **kwargs):
        super(Multi_Atttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout_rate)
        self.num_heads = num_heads
        self.attention = DotProductAttention(dropout_rate)
        self.W_q = nn.LazyLinear(num_hiddens)  # (batch_size, num_qkv, num_embeddings) -> (batch_size, num_qkv, num_hiddens)
        self.W_k = nn.LazyLinear(num_hiddens)
        self.W_v = nn.LazyLinear(num_hiddens)
        self.W_o = nn.LazyLinear(num_hiddens,bias=USEBIAS)  # (batch_size, num_q, num_hiddens) -> (batch_size, num_q, num_hiddens)

    def forward(self, q, k, v, valid_lens):
        q = transpose_qkv(self.W_q(q), self.num_heads)
        k = transpose_qkv(self.W_k(k), self.num_heads)
        v = transpose_qkv(self.W_v(v), self.num_heads)
        if valid_lens is not None:
            valid_lens = torch.repeat_interleave(valid_lens, self.num_heads, dim=0)
        output = self.attention(q, k, v, valid_lens)
        return transpose_output(output, self.num_heads)


def transpose_qkv(input, num_heads):
    """
    Input`s shape changes in this method
    1. Input (batch_size, num_qkv, num_hiddens)
    2. temp1 (batch_size, num_qkv, num_heads, num_hiddens/num_heads)
    3. temp2 (batch_size, num_heads, num_qkv, num_hiddens/num_heads)
    4. return (batch_size x num_heads, num_qkv, num_hiddens/num_heads)
    ---
    Multi Head but Single Head like in caculate
    enhance performence
    """
    _shape = input.shape
    _temp = torch.reshape(input, (_shape[0], _shape[1], num_heads, -1))  # temp1
    _temp = torch.permute(_temp, (0, 2, 1, 3))  # temp2
    _temp_shape = _temp.shape
    return torch.reshape(_temp, (-1, _temp_shape[-2], _temp_shape[-1]))

def transpose_output(output, num_heads):
    """
    Output shape changes in this method:
    Output: (batch_size x num_heads, num_q, num_hiddens/num_heads)
    temp1: (batch_size, num_heads, num_q, num_hiddens/num_heads)
    temp2: (batch_size, num_q, num_heads, num_hiddens/num_heads)
    return: (batch_size, num_q, num_hiddens)
    """
    _output_shape = output.shape
    _temp = torch.reshape(output, (-1, num_heads, _output_shape[-2], _output_shape[-1]))  # temp1
    _temp = torch.permute(_temp, (0, 2, 1, 3))  # temp2
    _temp_shape = _temp.shape
    return torch.reshape(_temp, (_temp_shape[0], _temp_shape[1], -1))



class DotProductAttention(nn.Module):
    """
    param:
    q: (n x d)
    k: (m x d)
    v: (m x d)
    out: (n x d)
    official：
    softmax(QK^T/d**0.5)V
    =====for example=====
    Input: (batch_size x num_heads, num_qkv, num_hiddens)
    Output: (batch_size x num_heads, num_q, num_hiddens)
    """
    def __init__(self, dropout_rate, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout_rate)

    def forward(self, q, k, v, valid_lens):
        _scores = torch.bmm(q, k.transpose(1, 2)) / math.sqrt(q.shape[-1])
        self.weights = masked_softmax(_scores, valid_lens)
        return torch.bmm(self.dropout(self.weights), v)

class Add_Norm(nn.Module):
    def __init__(self, normlized_shape, dropout_rate, **kwargs):
        super(Add_Norm, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout_rate)
        self.layerNorm = nn.LayerNorm(normlized_shape)
    def forward(self, X, Y):
        return self.layerNorm(self.dropout(Y)+X)


class PositionWiseFFN(nn.Module):
    def __init__(self, ffn_hiddens, ffn_ouputs):
        super().__init__()
        self.dense1 = nn.LazyLinear(ffn_hiddens)
        self.relu = nn.ReLU()
        self.dense2 = nn.LazyLinear(ffn_ouputs)

    def forward(self, X):
        return self.dense2(self.relu(self.dense1(X)))


def masked_softmax(X, valid_lens):
    """
    掩码注意力，valid_lens:有效长度
    ======Examples=====
    masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))
    tensor([[[0.5980, 0.4020, 0.0000, 0.0000],
         [0.5548, 0.4452, 0.0000, 0.0000]],

        [[0.3716, 0.3926, 0.2358, 0.0000],
         [0.3455, 0.3337, 0.3208, 0.0000]]])
    -------
    masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))
    tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
         [0.4125, 0.3273, 0.2602, 0.0000]],

        [[0.5254, 0.4746, 0.0000, 0.0000],
         [0.3117, 0.2130, 0.1801, 0.2952]]])
    """
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        X_shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, X_shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        X = sequence_mask(X.reshape(-1, X_shape[-1]), valid_lens, value=-1e6)
        return nn.functional.softmax(X.reshape(X_shape), dim=-1)

def sequence_mask(X, valid_len, value):
    """
    比较使用广播机制，先复制成相同的形状，再对应元素相比较
    maxlen表示填充后一句话有多少个字符，arange后则为每个字符的位置索引
    valid_len表示截断位置的索引标签，
    X为注意力分数，形状为(batch_size x num_qkv , num_v)，num_v表示对整个句子中其他字符的注意力
    广播：
    arange(maxlen)沿着hh方向广播，广播了(batch_size x num_qkv)行
    valid_len沿着列方向的广播，广播了num_v次
    每个样本比较表示对这个词的注意力超过截断位置没，超过返回False，否则返回True
    所以，经过广播得到的mask与X的形状相同，取反在超过截断位置的地方将X的值设置为value
    """
    maxlen = X.size(1)
    mask = torch.arange((maxlen), dtype=torch.float32,
                        device=X.device)[None, :] < valid_len[:, None]
    X[~mask] = value
    return X


if __name__ == '__main__':
    class vocab:
        idx2token = None
        token2idx = None
    with open("../data/wikitext-2/vocab.json", 'r') as myVocab:
        temp = json.load(myVocab)
        vocab.idx2token = temp["idx2token"]
        vocab.token2idx = temp["token2idx"]
    class dataSet(data.Dataset):
        def __init__(self, ptPath):
            super().__init__()
            dataset = torch.load(ptPath).values()
            self.sentence_pairs, self.segments, self.valid_lens, \
                self.masked_pos, self.masked_wights, \
                self.masked_tokens, self.nextSentenceLabel = dataset
        def __getitem__(self, idx):
            return (self.sentence_pairs[idx], self.segments[idx], self.valid_lens[idx],
                    self.masked_pos[idx], self.masked_wights[idx],
                    self.masked_tokens[idx], self.nextSentenceLabel[idx])
        def __len__(self):
            return len(self.sentence_pairs)

    dataset = dataSet("../data/wikitext-2/miniWiki.pt")
    trainIter = data.DataLoader(dataset, batch_size=32)

    devices = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    loss = nn.CrossEntropyLoss(reduction='none')
    num_steps, learning_rate = 50, 0.01
    loss_mlm, loss_pns, loss_add = [], [], []
    myBERT = BERTModel(vocab_size=len(vocab.idx2token), num_hiddens=32, num_heads=4, dropout_rate=0.3, ffn_hiddens=64, num_blks=2, max_len=1000, bias=True)
    def getBatchLoss(net, loss,
                     sentence_pairs, segments, valid_lens,
                     masked_pos, masked_weights,
                     masked_tokens, nextSentenceLabel):
        encoded_X, mlm_hat, pns_hat = net(sentence_pairs, segments, valid_lens, masked_pos)
        mlm_l = loss(mlm_hat.reshape(-1, mlm_hat.size(-1)), masked_tokens.reshape(-1))
        mlm_l = mlm_l.sum() / (masked_weights.sum() + 1e-8)
        pns_l = loss(pns_hat, nextSentenceLabel)
        pns_l = pns_l.mean()
        l = mlm_l + pns_l
        return mlm_l, pns_l, l

    def trainBert(train_iter, net, loss, device, num_steps, lr=learning_rate):
        net(*next(iter(train_iter))[:4])
        net = net.to(device)
        trainer = torch.optim.Adam(net.parameters(), lr=lr)
        step = 0
        while step < num_steps:
            for sentence_pairs, segments, valid_lens, \
                    masked_pos, masked_weights, \
                    masked_tokens, nextSentenceLabel in train_iter:
                sentence_pairs = sentence_pairs.to(device)
                segments = segments.to(device)
                valid_lens = valid_lens.to(device)
                masked_pos = masked_pos.to(device)
                masked_weights = masked_weights.to(device)
                masked_tokens = masked_tokens.to(device)
                nextSentenceLabel = nextSentenceLabel.to(device)
                trainer.zero_grad()
                start_time = time.time()
                mlm_l, pns_l, l = getBatchLoss(net, loss,
                                               sentence_pairs, segments, valid_lens,
                                               masked_pos, masked_weights,
                                               masked_tokens, nextSentenceLabel)
                l.backward()
                trainer.step()
                end_time = time.time()
                TimeUse = end_time-start_time
                print(f"num_steps {step+1}: \n"
                      f"mlm_l: {mlm_l}; \n"
                      f"pns_l: {pns_l}; \n"
                      f"loss: {l}; \n"
                      f"time: {TimeUse}. \n"
                      f"====================================================")
                loss_mlm.append(mlm_l.detach().numpy())
                loss_pns.append(pns_l.detach().numpy())
                loss_add.append(l.detach().numpy())
                step += 1
                if step == num_steps:
                    break

    trainBert(trainIter, myBERT, loss, devices, num_steps)

    step = [i+1 for i in range(num_steps)]
    plt.plot(step, loss_mlm, label='mlm_l')
    plt.plot(step, loss_pns, label='pns_l')
    plt.title('Train Loss')
    plt.legend()
    plt.show()
深度学习笔记
动手深度学习note-7(BERT-来自Transformer的双向编解码器表示)
https://blog.potential.icu/2024/04/28/2024-4-28-动手深度学习note-7(BERT-来自Transformer的双向编解码器表示)/
Author
Xt-Zhu
Posted on
April 28, 2024
Licensed under